배울 점이 많은 강의가 있어서 추천드리며, 시리즈로 글을 쓰고자 합니다.
비정형 데이터 분석 8/11 LDA Inference: Collapsed Gibbs Sampling
키워드 및 핵심 내용
LDA Inference: Collapsed Gibbs Sampling
- 관찰할 수 있는 문서와 단어로 숨겨진 토픽의 분포를 추정
- 나머지는 정리가 잘되었다고 가정하고 한 번에 하나씩 정리
1. 각각의 단어에 임의의 주제를 배정한다.
2. (잘못됐겠지만) 모든 단어에 주제가 배정되어 있고, 그 결과 문헌별 주제 분포와 주제별 단어 분포가 결정되었음. 이를 깁스 샘플링을 통해서 개선해 나간다.
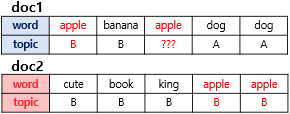
3. 문헌 A에 속하는 단어 cute가 주제1에 속할지 주제2에 속할지 판단해야 합니다. 문헌 내 주제 분포를 따르면
(문헌 A 내에 주제1이 있을 확률) = 0.1 / (0.1+1.1) = 0.083...
주제별 단어 분포를 따르면
(주제1 내의 단어가 cute 일 확률) = 0.001 / 8.007 = 0.00012...
따라서 (A 안의 cute가 주제1일 확률) = 0.083 * 0.00012 ... = 0.00008... 이 됩니다.
마찬가지로 주제2에 속할 확률도 계산해봅시다.
(문헌 A 내에 주제2가 있을 확률) = 1.1 / (0.1+1.1) = 0.916...
(주제2 내의 단어가 cute 일 확률) = 1.001 / 8.007 = 0.125...
따라서 (A 안의 cute가 주제2일 확률) = 0.916 * 0.125 ... = 0.114... 가 됩니다.
즉 A 안의 cute는 (0.00008, 0.114)의 카테고리 분포를 따라 주제1이 되거나 주제2가 되겠죠. 가능도 비중을 따라 주제1이나 주제2 중에 하나를 뽑습니다. (물론 높은 확률로 주제2가 뽑히겠죠. 하지만 주제1이 뽑힐 가능성이 아예 0이 되지는 않습니다. 이는 하이퍼 파라미터 α와 β가 하는 역할 중 하나에요.) 여기서는 주제2로 배정되었다고 가정할게요.
4. 다음 단어 반복

[Gibbs Sampling 추가 자료]
https://enginius.tistory.com/514
Bayesian과 MCMC 알고리즘 (Gibbs and Metropolis-Hastings Algorithm)
Motivation
깁스 샘플링이 무엇인가를 정의하기 전에 이것이 왜 필요한지에 대해서 먼저 생각해보자.
'우리'는 베이지안이라고 가정을 하겠다.
베이지안은 '일반적'으로 우리의 현상을 표현하는 latent variable을 가정한다.
우리의 현상, 혹은 관측을 Y라 하고, 이 현상의 원인을 X라 했을 때, 다음 세 가지를 정의한다.
- 편의상 X를 내면의 감정이라 하고, Y를 외면의 표현이라고 하자.
- X는 기쁨, 슬픔, 등등이 있고, Y에는 웃음, 울기, 짜증 등등이 있을 것이다.
1. Likelihood (개인적으로 우도란 단어를 별로 좋아하지 않는다.)
P(Y|X)
이것이 의미하는 것은 어떤 (원인)의도가 주어졌을 때 (관찰)현상이 일어날 확률이다. 예를 들면 슬플 경우 꽤나 높은 확률로 울 것이다.
2. Posterior
P(X|Y)
베이지안의 주된 목적은 바로 이것을 구하는 것이다. 다시 말해서 우리에게 현상이 주어졌을 때 원인을 찾는 것이다. 예를 들면 누가 웃고 있을 때 과연 이 사람이 슬픈지, 기쁜지를 알아내는 것이다. 이는 단순히 Likelihood와는 다르다. 현상에서 원인을 '역으로' 맞추는 것이기 때문에 추가 정보가 필요하고, 이것이 Prior이다. 이는 해당 사람이 평소에 슬픈지, 기쁜지에 대한 사전 정보이다.
3. Prior
P(X)
이것은 앞서 말한 사전 정보이다. 사람이 평소에 기쁜지, 슬픈지, 짜증 내는지에 대한 정보이다. 이 정보의 유무에 따라 베이지안과 프리퀀티스트를 나눈다고 볼 수 있다.
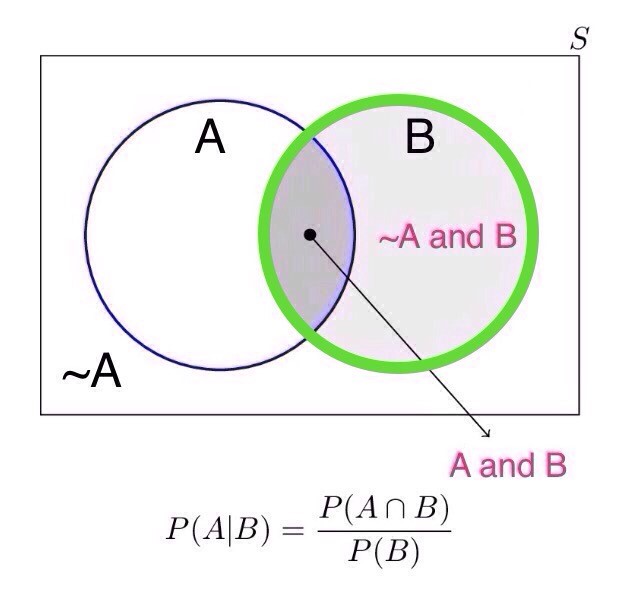
그리고, 위의 식들을 하나로 묶는 것이 바로 베이즈 법칙이다.

말로 풀어서 설명을 해보면 어떤 사람이 울고 있을 때 이 사람이 기쁠 확률은
1. 해당 사람이 기쁠 때 울 확률과
2. 해당 사람이 평소에 기쁠 확률을
곱해서 구해진다는 것이다. 나름 일리가 있다.
|
여기서 한 가지 주의할 점은 비례한다는 것이다. 정확한 확률 분포를 구하기 위해서는 normalize를 해줘야 하고, 이는.. 어렵다! 특정 Likelihood와 Prior가 곱해졌을 경우 Posterior를 쉽게 구할 수 있는 경우가 있는데 이런 Prior를 Conjugate Prior라고 한다. 대표적인 예로는 가우시안-가우시안+인버스 감마, 디리클레-멀티노미알 등이 있다. 자세한 건 위키를 참고하면 된다. |

위에서 설명한 Likelihood, Prior, Posterior에 대한(?) 그림
우리가 어떤 '값'을 원한다고 하자. 예를 들면 울고 있는 저 사람이 기쁠 '확률'을 구하시오! 혹은 이 사람이 기쁜지 슬픈지를 '구분'하시오! 란 명령이 내려졌다고 하자. 이런 경우에 베이지언은 다음과 같은 해답을 내놓는다.

즉 Posterior mean을 구한다는 의미이다. 그리고 이 적분은 가능한 모든 X의 공간인 X에서 수행되어야 한다. 하지만 우리가 모두 알듯이 적분은 어렵다. 그래서 이를 근사하고자 할 때 사용되는 것이 바로 Monte Carlo Markov Chain (MCMC) 알고리즘이다. 위의 적분은 큰 수의 법칙에 따라 다음과 같이 표현될 수 있다.

그리고 여기서 필요한 가정이

이다. 즉 우리가 모은 N 개의 데이터가 Posterior에서 '추출된' 데이터야 한다는 것이다.
하지만 이는 생각보다 쉽지가 않다. 여기에는 두 가지 이슈가 있다.
1. 우리가 추출할 수 있는 확률은 Uniform 혹은 Gaussian 정도이다.
2. 데이터의 차원이 커질수록 exponential 하게 어려워진다..
첫 번째 문제를 다루고 있는 것이 Metropolis-Hastings (MH) 알고리즘이고, 두 번째 문제를 다루고 있는 것이 Gibbs 샘플링이다.
Metropolis-Hastings (MH) Algorithm
알고리즘 자체는 매우 간단하고, 증명은 매우 복잡하니 알고리즘 설명만 하겠다. 여기서 증명이라는 것은 이런 식으로 뽑아도 괜찮다는 것을 의미한다.
1. 목적

가 주어졌을 때, pi(X)에서 N 개의 샘플인 X_1, X_2, ..., X_N 을 구하는 것이다.
2. 알고리즘
|
초기화 : 임의의 q(y|x)를 설정한다. 그리고 이는 우리가 sample 할 수 있어야 한다. 일반적으로 다음과 같이 설정한다. 의미를 생각해보면 현재 샘플 된 값 주변에서 다음 샘플을 뽑고자 하는 것이다. : 초깃값 X_1을 구한다. n-th 샘플링 1.에서 Y를 뽑는다. 2. 다음과 같이 r을 구한다. 이때 f는 pi에 비례하는 함수이다. 3. r의 확률로 X_n = Y로 하고, 1-r의 확률로 X_n = X_n-1로 한다. 사족 1: r의 의미를 살펴보면, 이 값은 Y가 우리의 분포인 pi(Y)에 대해서 얼마나 적합한지를 나타낸다. 분모에 f(Y)가 있으므로, 확률이 더 높은 걸 뽑으려고 하는 경향성을 볼 수 있다. 사실 우리는 X_i들을 다 모아서 empirical distribution을 그렸을 때 pi(·)이 되도록 하길 원하므로 일맥상통한다고 볼 수 있다. 사족 2: 여기서 f는 우리가 관심 있는 pi에 비례함에 주목하자. 바꿔 말하면 정확한 확률 분포가 아니라 비례하는 pseudo-distribution이여도 이 알고리즘은 돌아갈 수 있다. |
위의 알고리즘에서 알 수 있듯이 우리는 우리의 목적인 pi(X)에서 X를 직접 뽑을 필요가 없다. 하지만 이 알고리즘은 데이터의 차원이 커질수록 매우 오랜 시간이 걸려서 알고리즘이 돌아간다.
자세한 것은 위키(http://en.wikipedia.org/wiki/Metropolis–Hastings_algorithm)를 참고하도록 하자.
Gibbs Sampling
1. 목적
깁스 샘플링에 대한 포스팅은 예전에 한 적이 있다. (http://enginius.tistory.com/296) 벌써 2년 전이다.. 시간 참 빠르다. 여튼 깁스 샘플링의 의의(?)는 고차원 공간에서 샘플링을 효과적으로 할 수 있다는 데 있다. 사실 개념은 굉장히 straight-forward 하다. d 차원의 랜덤 변수를 d 개의 1차원 변수로 나눠서 보겠다는 것이다.
2. 알고리즘
|
우리가 관심 있는 것이 X = {x_1, x_2, ..., x_d}의 d 차원 변수라고 할 때, 이들을 나눠서 샘플링 하면 된다. 즉, 를 잘 정의하고, i = 1, 2, ..., d로 반복하면서 X를 뽑는다. 간단하다. 물론 여기서 위의 확률 분포에서 뽑기가 힘들 땐, 앞서 설명한 Metropolis-Hastings 알고리즘을 이용하면 된다. |
정리하자면 임의의 다차원 확률 분포가 주어졌을 때, 이들을 conditional distribution으로 변경할 수 있다면, Metropolis-Hastings 알고리즘과 Gibbs sampling을 이용해서 이들 분포를 따르는 확률분포의 seqeunce를 뽑아낼 수 있고, Posterior mean을 구할 수 있다.
[베이즈 정리 추가 자료]
https://m.blog.naver.com/davidj09/221246165061






[Gibbs Sampling 추가 자료]
https://newsight.tistory.com/102
MCMC, Metropolis-Hastings, Gibbs Sampling
by 곽동현 IMCOMKING 2014. 7. 22.
Markov Assumption(=Markov Property) : 직전 사건에 의해서만 현재 사건이 영향을 받는 속성
Chain : discrete 한 Time Sequence 사건
Markov Chain : Markov Assumption 을 만족하는 Chain
Monte Carlo Method : 다음과 같이 여러 개의 표본을 추출해서 전체적인 분포를 파악하는 방법론

Sampling : 해당 모델을 만족하는 데이터를 생성, 추출해내는 것. 단 그 모델의 확률 분포에 비례하여 확률 밀도가 높은 곳에서 그에 비례하게 더 많은 데이터가 나오도록 추출해야 한다.
Markov Chain Monte Carlo : Markov Chain에서 샘플링을 하기 위해 Monte Carlo Method를 써서 확률 분포가 반영된 데이터를 샘플링하는 것. 여기서의 Markov는 샘플링을 Markov Chain으로 하는 의미임.
(Markov Random Field에서의 Markov는 그래프의 노드들이 서로 마르코프 프로퍼티를 갖는 의미인 듯)

Detailed Balance : MCMC에서 뽑은 샘플이 P(X)의 분포를 충분히 근사하기 위한 조건. P(X'->X)/P(X->X')=1 이면 만족하며, Ergodicity라는 개념 또한 관련이 있다. 간단히 말하면 확률 분포가 연속적이고 섬처럼 동떨어진 분포가 있지 않는 일반적인 경우를 말한다.
Rejection Sampling : MCMC 알고리즘 중 가장 기본적인 샘플링 기법. 랜덤하게 (Uniform 하게) 하나의 데이터를 추출한 다음, 그것의 확률 값을 계산하여 그 확률만큼 Accept 하고 나머지는 Reject 시키는 방법. (당연히 이렇게 하면 확률 값이 큰 곳의 샘플들은 많이 뽑히고, 확률 값이 적은 곳의 샘플들은 잘 뽑히지 않는다. 그러나 이 방법은 확률분포가 매우 넓고 길게 퍼져있는 공간에서는 버려야 하는 샘플이 너무 많아 시간 효율이 좋지 않다.)
Metropolis-Hastings : 조금 더 개선된 MCMC 알고리즘의 하나로 샘플링을 한 번 한 다음, 다음 샘플에 대해서 Accept 할지를 min(1, P(X')/P(X)) 의 확률로 결정하는 방법. X'은 다음에 샘플링하기 위해 랜덤하게 (Uniform 하게) 뽑아본 샘플이다. min(1, P(X')/P(X))을 해석해보면, X'에서의 확률이 기존 샘플 X에서의 확률보다 크면 무조건 샘플링을 하는 것이고(1이 선택되므로),X'의 확률이 더 작은 경우 그에 비례하여 Reject를 하는 방법이다. 이것은 Detailed Balance를 만족시키면서 보다 빠른 방법이다.
그러나 Metropolis-Hastings의 경우도 고차원으로 갈수록 한 샘플에서의 확률 값이 0으로 점점 가까워지기 때문에 Accept Ratio가 매우 낮아져 시간 상 비효율적이다.
(고차원에서도 어떤 확률 분포의 합은 결국 1이 되어야 한다. 그러나 차원이 커질수록 그것을 구성하는 분포도 차원에 따라 확장되어 퍼질 수밖에 없다.)
Gibbs Sampling : Metropolis-Hastings의 단점인 고차원에서의 느린 샘플링을 해결한 MCMC 알고리즘. 구현이 쉽고 간편하며, 실행 속도도 빨라 널리 사용되는 샘플링 방법이다.
맨 처음 하나의 Initial 한 샘플을 랜덤하게 정한 다음, 그 샘플에서 변수를 1개씩, 즉 1개 차원씩 번갈아가면서 정하는 방법.
이것은 Xi ~ P(Xi|X-i) 로 표현하며, 의미는 Xi라는 i 번 째 변수 하나를 결정할 때, i를 제외한 나머지(X-i) 변수들을 이용해서 결정하는 것이다.
만약 L 차원에서의 확률 분포라면, 1~L까지의 변수들을 하나씩 샘플링 한 다음, 다시 1~L까지를 또 샘플링하고 이것을 계속해서 반복한다. 그렇게 만든 샘플들이 쭉 있으면, 그것들을 다시 일정한 간격으로 택하여 최종 샘플링을 완성한다.
Gibbs Sampling은 고차원의 영역을 빠르게 여기저기 왔다 갔다 하면서 샘플들을 뽑기 때문에 딥러닝 등에서 자주 쓰인다.
(Gibbs Sampling의 Binary에서 예시)
1-1 : [1,0,1] // Initial 샘플로, 랜덤하게 정해진 것이며, 굵게 칠해진 숫자"1"을 0으로 바꿀지, 그대로 1로 놓을 지를 나머지 두 변수 0, 1의 확률을 이용해서 계산한다.
1-2 : [0,0,1] // 다시 두 번째 변수인 0에 대해서 결정 한다. 물론 확률적인 것으로, 0->0이 될 수도 있고 0->1이 될 수도 있다.
1-3 : [0,1,1] // 마지막 세 번째 변수인 1에 대해서 정한다. 이번엔 1->1로 변하지 않았다.
(3차원 변수이므로, 3회가 지날 때마다 전체 데이터를 샘플링한다.)
2-1 : [0,1,1] // 다시 마지막 상태에서부터 이어서 첫 번째 변수부터 시작한다.
2-2 : [1,1,1]
...
이렇게 1000사이클을 돌아 총 1000*3개의 결과가 완성되었다고 해보자, 그러면 이 3천 개의 데이터 셋에서 일정한 간격(N 차원 일 경우, N 번 째 간격)으로 데이터를 선택하여 최종적인 샘플링을 완성한다. 그 이유는 위와 같은 과정이 N 번 거쳐야만, 모든 차원에 대해 변화가 이루어지기 때문이다.
Gibbs Sampling은 일종의 현재 상태에서의 변수들의 상태를 체크해보고자 하는 방법으로 쓰일 것 같다는 느낌이다. 물론 활용 범위가 매우 매우 커서 공학적으로 안 쓰이는 곳이 없는 것 같다.
http://enginius.tistory.com/296
고급이론 :
Gibbs sampling에서는 proposal distribution 이 그 확률 분포 자체의 conditional distribution이다. RBM 같은 경우 이 conditional 분포 자체가 gaussian 혹은 베르누이 분포이기 때문에 이 자체에서도 바로 샘플링이 가능하며, 이것의 의미는 N 차원의 공간에서 1축씩 이동할 때, conditional distribution을 통해서 샘플링을 하여 한 축씩 이동하는 것을 의미한다.
그런데 만약 gibbs sampling에서의 conditional distribution 자체만으로 proposal distribution으로 사용이 불가능할 때, 즉 샘플링이 불가능한 분포인 경우 이 1개의 축을 이동하는 과정에서도 metropolis-hastings 같은 방법을 사용해야만 한다. 즉 어떻게 보면 깁스 샘플링은 1축씩 이동하는 어떤 메타 방법론이라고 볼 수도 있다.
그리고 만약 gibbs sampling을 2차원의 변수에 대해서 할 때, 2개의 모드가 있는데 이 두 개의 모드가 x1과 x2의 대각선 방향으로 아주 멀리 서로 위치해 있다면, gibbs sampling만으로는 절대 다른 모드로 넘어갈 수가 없다. 왜냐하면 1축씩 이동하는 방식으로는 현재의 모드 밖을 넘어갈 확률이 0이기 때문이다.(대각선에 위치하므로 1개의 변수만 사용해서는 확률이 0이 됨)
그러나 아주 고차원 공간에서는 이런 식으로 모든 축에 대해서 걸리지 않는 모드가 존재할 확률이 매우 낮아지고, 반드시 어느 한 축에서는 다른 모드의 확률이 존재하게 된다. 그래서 고차원 공간에서는 이렇게 1개의 축이라도 걸리면, 이 축을 통해서 다른 모드로 넘어가는 것이 가능하다. 그래서 gibbs sampling이 고차원 공간에서 아주 빠르게 효과적으로 잘 동작한다고 볼 수 있다.
https://newsight.tistory.com/151
Gibbs sampling
MCMC는 N 차원의 점에서 바로 N 차원의 점으로 모든 차원을 한 번에 이동하면서 샘플링을 한 것인 반면, 깁스 샘플링은 한 개의 차원을 제외한 나머지는 고정을 시킨 다음, 한 차원 씩 샘플링을 해서 총 N 번의 이동을 하고 난 다음 진짜 새로운 데이터를 샘플링하는 것이다.
단 깁스 샘플링을 하기 위해서는 말한 대로 한 개 차원을 제외한 나머지를 given으로 고정시켜야 한다. 즉 각 차원에 대한 conditional probability를 알아야만 사용이 가능하다.
그러나 RBM 같은 모델의 경우, 우리가 모델을 정의하였으므로 그 conditional probability를 알 수가 있다. 따라서 당연히 깁스 샘플링도 가능하다.
MH는 1~10차원의 샘플링은 잘 하지만, 수천 차원에서의 샘플링은 리젝션 레이트가 너무 높아서 작동을 하지 못한다.
깁스 샘플링이 좋은 이유는 한 번에 1개의 차원씩 이동을 하기 때문에, 문제를 훨씬 단순화 시켜서 풀었다는 것이고 그로 인해 고차원의 저주와 같은 문제가 안 발생하는 걸로 보인다. 그래서 고차원 분포의 샘플링에서 훨씬 빠르게 동작하는 것 같다.
[Gibbs Sampling 추가 자료]
https://bab2min.tistory.com/569
문헌 d에 속하는 어떤 단어 m이 주제 j에 속할 확률은 주제 j에 속하는 모든 단어 중에서 단어 m이 차지하는 비중과 문헌 d에 속하는 모든 주제 중 주제 j가 차지하는 비중의 곱에 비례한다는 것입니다.
깁스 샘플링을 이용한 LDA는 다음과 같은 절차로 이뤄집니다.
1. 각각의 단어에 임의의 주제를 배정한다
2.(잘못됐겠지만) 모든 단어에 주제가 배정되어 있고, 그 결과 문헌별 주제 분포와 주제별 단어 분포가 결정되었음. 이를 깁스 샘플링을 통해서 개선해 나가자.
3.n 번째 단어를 골라 빼낸다. (나머지 단어들이 모두 적절하게 배정되어 있다고 가정하고)
4. 빼낸 단어를 제외하고, 그 단어가 속한 문헌의 주제 분포(P(Topic | Document))를 계산하고, 그 단어가 속한 주제의 단어 분포(P(Word | Topic))를 계산한다. P(Word | Topic) * P(Topic | Document)에서 Topic을 하나 뽑아 그 단어에 배정한다.
5.n <- n+1로 하고 3번으로 돌아간다.
6. 충분히 반복하다 보면 값들이 수렴하고 안정되게 된다. 그럼 끝.
적용예)
|
1. 각각의 단어의 임의의 주제를 배정한다 |
주제가 2개이므로 #1, #2둘 중에 하나를 각 단어에 임의로 배정했습니다. 이렇게 단어가 배정되었으니 우리는 이제 문헌별 주제 분포와 주제별 단어 분포를 계산할 수 있습니다.
|
2. 문헌별 주제 분포, 주제별 단어 분포를 계산한다. |
문헌별 주제 분포 θ입니다. 각 값이 0으로 끝나는 게 아니라. 1인 이유는 모든 값에 하이퍼 파라미터 α값이 합쳐져 있기 때문입니다. A 문헌에는 #1, #2가 각각 하나씩이므로 (1.1, 1.1)이 계산된 것이고, C 문헌에는 #2만 2개 배정되었으므로 (0.1, 2.1)가 계산된 것입니다.
주제별 단어 분포 φ입니다. 마찬가지로 0.001로 끝나는 이유는 하이퍼 파라미터 β값이 합쳐져 있기 때문입니다.
|
3. 첫 번째 단어를 골라 빼낸다. |
첫 번째 단어 cute를 빼냈습니다. 따라서 문헌별 주제 분포, 주제별 단어 분포도 다음과 같이 바뀌게 됩니다.
|
4. 새로운 주제를 배정한다 |
문헌 A에 속하는 단어 cute가 #1에 속할지 #2에 속할지 판단해야 합니다. 문헌 내 주제 분포를 따르면
(문헌 A 내에 #1이 있을 확률) = 0.1 / (0.1+1.1) = 0.083...
주제별 단어 분포를 따르면
(#1 내의 단어가 cute 일 확률) = 0.001 / 8.007 = 0.00012...
따라서 (A 안의 cute가 #1일 확률) = 0.083 * 0.00012 ... = 0.00008... 이 됩니다.
마찬가지로 #2에 속할 확률도 계산해봅시다.
(문헌 A 내에 #2가 있을 확률) = 1.1 / (0.1+1.1) = 0.916...
(#2 내의 단어가 cute 일 확률) = 1.001 / 8.007 = 0.125...
따라서 (A 안의 cute가 #2일 확률) = 0.916 * 0.125 ... = 0.114... 가 됩니다.
즉 A 안의 cute는 (0.00008, 0.114)의 카테고리 분포를 따라 #1이 되거나 #2가 되겠죠. 가능도 비중을 따라 #1이나 #2 중에 하나를 뽑습니다. (물론 높은 확률로 #2가 뽑히겠죠. 하지만 #1이 뽑힐 가능성이 아예 0이 되지는 않습니다. 이는 하이퍼 파라미터 α와 β가 하는 역할 중 하나에요.) 여기서는 #2로 배정되었다고 가정할게요.
|
3-1. 두 번째 단어를 골라서 빼낸다. |
여기서부터는 반복입니다. 설명은 다 적지 않도록 하고 각 단어 샘플링 단계마다 주제 배정이 어떻게 바뀌었는지만 보여드리도록 하겠습니다.
두 번째 단어 업데이트. #2에 배정됨
세 번째 단어 업데이트. #1에 배정됨
네 번째 단어 업데이트. #1에 배정됨
.
마지막 단어까지 업데이트가 끝나면 이것이 1회 깁스 샘플링을 마무리한 것이 됩니다. 이 작업을 적절하게 여러 번 반복하다 보면 모든 단어가 적절하게 자기 주제를 찾아 배정되게 될 것이라는 것이 깁스 샘플링을 이용한 LDA의 가정이죠. 수렴할 때까지 반복하면 다음과 같은 결과가 나옵니다.
최종 결과물
이를 바탕으로 구한 문헌별 주제 분포, 주제별 단어 분포는 다음과 같습니다.
이를 보기 좋게 정리하면 다음과 같이 되겠죠.
#1: eat(0.272), cake(0.272), bread(0.272), rice(0.181), cute(0.001), kitty(0.001) hamster(0.001)
#2: cute(0.333), kitty(0.333), hamster(0.333), eat(0.001), rice(0.001), cake(0.001), bread(0.001)
적절하게 잘 분류된 것 같군요. #1에는 '음식'이라는 타이틀을, #2에는 '귀여운 동물'이라는 타이틀을 붙여주면 딱 좋겠군요.
[이은아님 강의 모음]
https://www.youtube.com/playlist?list=PLGAnpwASolI0vViZItiP90nWI_s9m91Av


'머신러닝' 카테고리의 다른 글
| 머신러닝으로 투자에 성공할 수 있을까? (0) | 2020.07.16 |
|---|---|
| [추천강의] 이은아님 머신러닝 비정형 데이터 분석 9/11 Seq2Seq, Attention (0) | 2020.07.15 |
| [추천강의] 이은아님 머신러닝 비정형 데이터 분석 7/11 토픽모델링 LDA (0) | 2020.07.11 |
| [추천강의] 이은아님 머신러닝 비정형 데이터 분석 6/11 Topic Modeling: pLSA (0) | 2020.07.10 |
| [추천강의] 이은아님 머신러닝 비정형 데이터 분석 5/11 Feature Extraction t-SNE (0) | 2020.07.09 |